본 포스팅에서는 머신러닝 손실함수의 최적화 알고리즘인 '경사하강법'에 대해 알아보겠습니다.
1. 손실함수의 최적화
경사 하강법(Gradient Descent Algorithm)
└ Cost 를 최소화 시키는 Parameter를 찾는 최적화 알고리즘입니다.
└ 함수의 기울기(Gradient)를 구하여 기울기가 낮은 쪽으로 계속 이동시켜서 극값(minimum)에 이를 때까지 반복 수행하여 구할 수 있습니다.
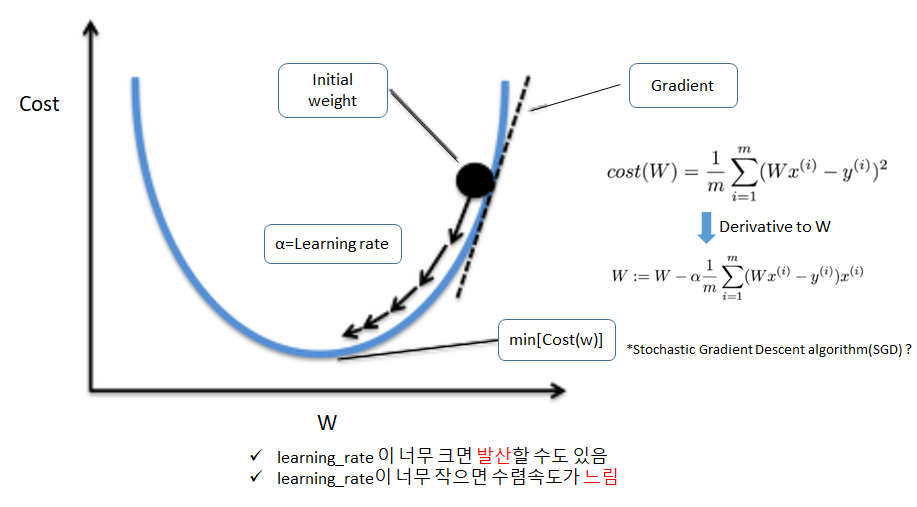
앞선 포스팅에서 알아본 MSE(mean square error) 손실 함수는 그림1과 같이 convex function인 2차함수로 나타낼 수 있습니다.
새로운 가중치 (W')는 이전 가중치(W)에서 손실함수의 가중치에 대한 미분값에 상수(ρ)를 곱한 값의 합으로 업데이트 됩니다.
상수(ρ)는 Learning rater라고 하며, 계산한 기울기를 얼만큼 반영할 것인가를 결정하는 factor라고 할 수 있습니다.
예를들어 이전 기울기가 0.5, 손실 함수의 기울기가 0.3 일때,
ρ가 0.1일 경우에는 새로운 가중치가 0.5 - (0.1)(0.3) = 0.47
ρ가 0.9일 경우에는 새로운 가중치가 0.5 - (0.9)(0.3) = 0.23
이 됩니다.
즉 ρ 값이 커질수록 업데이트 속도가 빠르고, 값이 작을수록 느리게 업데이트 된다고 할 수 있습니다.
ρ 값이 크다고 무조건 유리하지 않은 이유는, minimum 값에 수렴하지 않고 특정 구간에서 발산할 위험이 있기 때문입니다
반복은 min값을 threshold로 지정하여 도달할때까지 반복할 수도 있고, iteration 횟수를 지정하여 특정 횟수만큼 가중치 업데이트를 할 수도 있습니다.
SGD가 GD와 구분되는 내용은 손실함수를 계산할때 사용되는 batch 크기 입니다. GD는 전체 data에 대해 손실함수를 계산하는 반면 SGD는 random하게 특정 batch를 선별하여 손실함수를 계산합니다. 따라서, SGD는 GD에 비해 계산량이 훨씬 줄어드는 반면 기울기가 bias되어 나타나므로 기울기가 급격하게 업데이트 된다는 특징이 있습니다.
Convex function, GD는 손실함수가 볼록함수(convex function)으로 최소값을 갖는다는 전제를 갖고 수행됩니다. 따라서 실제 손실함수가 울퉁불퉁한 형태의 함수인 경우, 실제 최소값이 아니라 특정 구간에 수렴되어 버리는 local minima 문제가 나타날 수 있습니다.
2. Gradient Descent algorithm의 응용

[1]. Stocastic Gradient descent algorithm
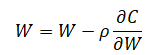
배치 단위로 손실함수의 gradient를 계산하여 업데이트 하는 것을 말합니다.
때문에 계산량이 대폭 줄어든다는 이점이 있으며, 기울기가 급격하게 변하는 특징을 갖습니다.
[2]. Momentum
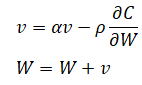
이전 기울기의 모멘텀(v)을 반영하므로, 기울기의 움직임이 둔화(그림2의 [2]) 되는 것을 확인 할 수 있습니다.
[3]. Adagrad
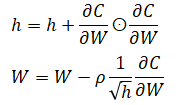
이전 기울기를 제곱하여 계속 더하(h)므로, 학습이 진행될수록 갱신강도가 약해지는 특징이 있습니다.
rmsprop과 조합하여 단순 누적이 이나라, 이전 값과 현재값이 일정 비율로 누적되도록 하기도 합니다.
[4]. Adam
Momentum + Adagrad
모멘텀과 Adagard의 특징을 조합한 방법으로, 이전 기울기의 모멘텀 반영하는 동시에 점차 갱신속도를 adaptive하게 조절하는 특징을 갖습니다.
이상으로 경사하강법 (gradient descent algorithm)에 대한 포스팅을 마치겠습니다.
다음 포스팅에서는 back propagation의 업데이트 원리에 대해 알아보겠습니다.
'머신러닝(Machine Learning)' 카테고리의 다른 글
| [Machine Learning] Batch normalization tips (0) | 2021.03.25 |
|---|---|
| 어떻게 컴퓨터가 사진을 인식하는가 (0) | 2020.10.04 |
| [머신러닝] 선형 회귀 (Linear Regression) (0) | 2020.04.11 |